Division
- Flip the second fraction (reciprocal)
- Then multiply
4/5 ÷ 2/3 = 4/5 × 3/2 = 12/10 = 6/5
Patterns and Sequences
A pattern is a regular and repeated way in which numbers, shapes, or objects change. A sequence is an ordered list of numbers that follows a specific rule.
Sequences are important because they help us identify relationships, predict future values, and describe mathematical rules.
Arithmetic and Geometric Sequences
A sequence is an ordered list of numbers that follows a clear rule.
Each number in the sequence is called a term.
The position of a term is represented by n.
The two most important types of sequences studied in MYP are:
- Arithmetic sequences (add or subtract)
- Geometric sequences (multiply or divide)
1. Arithmetic Sequences
An arithmetic sequence is a sequence in which the
difference between consecutive terms is constant.
This constant value is called the common difference, written as d.
Identifying an Arithmetic Sequence
To check whether a sequence is arithmetic:
- Subtract consecutive terms
- If the difference is the same each time, the sequence is arithmetic
Example:
7, 12, 17, 22, 27, …
- 12 − 7 = 5
- 17 − 12 = 5
- Common difference,
d = 5
Arithmetic sequences can be:
- Increasing if
d > 0 - Decreasing if
d < 0
2. Finding the nth Term of an Arithmetic Sequence
The general formula for the nth term of an arithmetic sequence is:
Tₙ = a + (n − 1)d
a= first termd= common differencen= term number
Worked Example
Find the nth term rule for the sequence:
4, 9, 14, 19, …
Step 1: Identify a and d
First term, a = 4
Common difference, d = 5
Step 2: Substitute into the formula
Tₙ = 4 + (n − 1)5
Step 3: Simplify
Tₙ = 5n − 1
This rule allows us to find any term without listing the sequence.
3. Geometric Sequences
A geometric sequence is a sequence in which each term
is found by multiplying or dividing the previous term
by a constant value called the common ratio, written as r.
Identifying a Geometric Sequence
To check whether a sequence is geometric:
- Divide consecutive terms
- If the ratio is constant, the sequence is geometric
Example:
3, 6, 12, 24, 48, …
- 6 ÷ 3 = 2
- 12 ÷ 6 = 2
- Common ratio,
r = 2
4. Finding the nth Term of a Geometric Sequence
The general formula for the nth term of a geometric sequence is:
Tₙ = a × rⁿ⁻¹
a= first termr= common ration= term number
Worked Example
Find the nth term rule for the sequence:
5, 15, 45, 135, …
Step 1: Identify a and r
a = 5
r = 3
Step 2: Substitute into the formula
Tₙ = 5 × 3ⁿ⁻¹
5. Arithmetic vs Geometric Sequences
- Arithmetic sequences change by adding or subtracting
- Geometric sequences change by multiplying or dividing
- Arithmetic growth is linear
- Geometric growth is exponential
6. Applying Sequences in Real-Life Situations
a) Arithmetic Sequence Example (Salary Increase)
A worker earns ₹30,000 in the first year. Each year, their salary increases by ₹2,000.
This forms an arithmetic sequence:
30,000, 32,000, 34,000, 36,000, …
The nth-year salary can be found using:
Tₙ = 30000 + (n − 1)2000
b) Geometric Sequence Example (Population Growth)
A bacteria population doubles every hour. The initial population is 500.
This forms a geometric sequence:
500, 1000, 2000, 4000, …
The population after n hours is:
Tₙ = 500 × 2ⁿ⁻¹
This model is used in science, finance, and economics.
3. BODMAS (Fractions & Decimals)
- B – Brackets (solve inside brackets first)
- O – Orders (powers and roots)
- D – Division
- M – Multiplication
- A – Addition
- S – Subtraction
⚠️ Division and multiplication are done from left to right. Addition and subtraction are also done from left to right.

(3/4 + 1/2) × 8
Step 1: Solve the bracket
(3/4 + 1/2) = (3/4 + 2/4) = 5/4
Step 2: Multiply
5/4 × 8 = 10
Common Mistakes
- Ignoring brackets
- Doing addition before multiplication
- Forgetting to convert fractions to a common denominator
- Not following left-to-right order for × and ÷
Practice Questions
- (1/2 + 3/4) × 8
- 6 + 3 × 1/2
- (5 − 2/5) ÷ 3
- 4 + 2² × 1/2
- (0.6 + 1.4) ÷ 2 × 5
4. LCM and HCF (Criterion D)
Highest Common Factor (HCF)
- Largest number that divides two or more numbers
- Used for simplifying fractions
Lowest Common Multiple (LCM)
- Smallest number that is a multiple of two or more numbers
- Used when adding or subtracting fractions
Find HCF and LCM of 12 and 18
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
HCF = 6
LCM = (12 × 18) ÷ 6 = 36
Tips & Tricks
- HCF is useful to simplify fractions to lowest terms
- LCM is important for adding/subtracting fractions with different denominators
- Prime factorization is a reliable method for both HCF and LCM
- Always check by multiplying HCF and LCM: HCF × LCM = product of the numbers
Practice Questions
- Find HCF and LCM of 15 and 20
- Find HCF and LCM of 8 and 12
- Find HCF and LCM of 9 and 18
- Find HCF and LCM of 14 and 35
- Find HCF and LCM of 24 and 36
5. Terminating & Non-Terminating Decimals
Terminating Decimals
- End after a finite number of digits
- Can be written as fractions easily
0.25 = 25/100 = 1/4
Recurring (Non-Terminating) Decimals
- Digits repeat forever
- Use algebra to convert
Let x = 0.333…
10x = 3.333…
10x − x = 3
9x = 3 → x = 1/3
Practice Questions
- Convert 0.75 to a fraction
- Convert 0.125 to a fraction
- Convert 0.666… to a fraction
- Convert 0.142857… to a fraction
- Convert 0.8 repeating (0.888…) to a fraction
6. Significant Figures
- All non-zero digits are significant
- Zeros between numbers are significant
- Leading zeros are NOT significant
0.00456 → 3 significant figures
4050 → 3 significant figures
Practice Questions
- Find the significant figures of 0.00789
- Find the significant figures of 56007
- Find the significant figures of 0.009400
- Find the significant figures of 1200
- Find the significant figures of 0.03450
7. Squares and Square Roots
Square
- A number multiplied by itself
- Example: 7² = 49
Square Root
- The number that multiplies by itself to give the original number
- √49 = 7
Practice Questions
- Find the square of 12
- Find the square root of 144
- Find the square of 15
- Find the square root of 196
- Find the square of 8
8. Square Roots by Prime Factorization
Find √72
72 = 2 × 2 × 2 × 3 × 3
Pair equal numbers:
√72 = 2 × 3 × √2 = 6√2
Practice Questions
- Find √50 using prime factorization
- Find √98 using prime factorization
- Find √180 using prime factorization
- Find √200 using prime factorization
- Find √288 using prime factorization
9. Laws of Exponents
- am × an = am+n
- am ÷ an = am−n
- (am)n = amn
- a0 = 1
- a−n = 1 / an
2³ × 2⁴ = 2⁷ = 128
Practice Questions
- 3² × 3⁵
- 5⁷ ÷ 5³
- (2³)⁴
- 7⁰
- 4−2
IB MYP 2 – Unit 2: Statistics and Probability
1. Terminology in Statistics
- Data: Information collected for a purpose
- Observation: Each individual value in a data set
- Population: The complete group being studied
- Sample: A part of the population
- Discrete data: Countable data (e.g. number of students)
- Continuous data: Measured data (e.g. height, weight)
- Frequency: Number of times a value occurs
Practice Questions
- Identify the population and sample in a survey of student heights.
- Give an example of discrete data in your classroom.
- Give an example of continuous data.
- Define frequency for the number of pets owned by students.
- Classify each type of data (discrete/continuous) for number of books read per month.
2. Data Collection and Generation
Methods of Data Collection
- Surveys and questionnaires
- Interviews
- Observation
- Experiments
Good Surveys
- Questions must be clear and unbiased
- Sample size should be reasonable
- Questions should be relevant to the aim
Practice Questions
- Design a small survey to find students’ favourite fruit.
- List two advantages of using interviews over surveys.
- Give one example of data you could collect by observation.
- Why is sample size important in a survey?
- Give an example of a biased question and explain why it is biased.
3. Tally Marks and Frequency Table
Tally marks are used to record data quickly.
| Value | Tally | Frequency |
|---|---|---|
| Red | |||| | 4 |
| Blue | ||||| | | 6 |
Practice Questions
- Record the following data using tally marks: {2, 3, 3, 4, 2, 3, 4, 4}
- Complete a frequency table for the number of pets owned by students: {1, 2, 2, 1, 3, 2, 1}
- Convert the tally marks ||| ||| |||| into a frequency table.
- Explain why tally marks are useful for quick data recording.
- Draw a tally chart for the colors: Red, Green, Blue with counts {3, 5, 2}
4. Graphical Representation of Data
Bar Graph
- Used for discrete or categorical data
- Bars have equal width and gaps
Double Bar Graph
- Compares two related data sets
- Bars are placed side by side
Pie Chart
- Shows data as parts of a whole
- Total angle = 360°
Histogram
- Used for continuous data
- No gaps between bars
- Area represents frequency
Practice Questions
- Draw a bar graph for the following data: {Apples: 5, Oranges: 8, Bananas: 3}
- Create a double bar graph comparing two classes’ test scores.
- Calculate the angles for a pie chart if frequencies are {10, 15, 25}.
- Draw a histogram for continuous data: {2–4: 3, 4–6: 5, 6–8: 2}
- Explain why a histogram has no gaps between bars.
5. Frequency Polygon
- Constructed from a histogram
- Plot midpoints of class intervals
- Join points using straight lines
Practice Questions
- Draw a histogram and frequency polygon for the data: {1–2: 2, 2–3: 5, 3–4: 3}
- Identify the midpoints for class intervals: 5–10, 10–15, 15–20
- Explain why frequency polygons are useful compared to histograms
- Plot a frequency polygon for this histogram: {2–4: 4, 4–6: 6, 6–8: 2}
- Describe how to join the points for a frequency polygon correctly
6. Mean, Median, Mode, and Range
Mean
Average of the data
Median
- Middle value when data is arranged in order
- If even number of values → mean of two middle values
Mode
- Most frequently occurring value
Range
Practice Questions
- Find the mean of {4, 7, 9, 2, 6}
- Find the median of {12, 5, 8, 3, 10}
- Find the mode of {3, 5, 3, 7, 8, 3}
- Calculate the range of {15, 22, 19, 10, 18}
- Explain why the median is less affected by extreme values than the mean
7. Finding Mean Using Variables
When data includes variables, use algebra.
Mean of x, x+2, x+4 is 10
(x + x+2 + x+4) ÷ 3 = 10
3x + 6 = 30
x = 8
Practice Questions
- Find x if the mean of x, x+3, x+6 is 12
- Find x if the mean of 2x, x+4, 3x is 10
- Find the mean of 5, x, x+2, given mean = 8
- Find x if the mean of x, 2x, 3x, 4x = 10
- Check your answer: mean of x, x+1, x+2 = 7, find x
8. Stem and Leaf Diagram (Single)
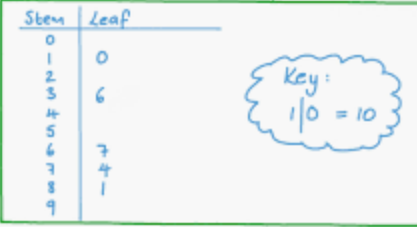
- Shows original data values
- Stem = first digit(s)
- Leaf = last digit
Data: 12, 15, 18, 21, 24
Stem | Leaf
1 | 2 5 8
2 | 1 4
Practice Questions
- Draw a stem-and-leaf diagram for {11, 14, 16, 19, 22, 24}
- Identify the stem and leaf for each data value in {13, 15, 17, 20}
- From the stem-and-leaf diagram, list all the original data values
- Explain why stem-and-leaf diagrams are useful for small datasets
- Create a stem-and-leaf diagram for {5, 7, 9, 12, 14, 16}
9. Sample Space
- Set of all possible outcomes of an experiment
- Written using brackets
Tossing a coin:
Sample Space = {H, T}
Practice Questions
- List the sample space for rolling a 6-sided die
- List the sample space for tossing two coins
- Write the sample space for picking a card from {A, B, C, D}
- List the sample space for spinning a spinner with numbers 1–4
- Identify the sample space for selecting a day of the week at random
10. Probability Scale
Probability values range from 0 to 1.
- 0 → Impossible
- 0.5 → Even chance
- 1 → Certain
Practice Questions
- State whether these events are impossible, even chance, or certain: Tossing a coin and getting heads, Rolling a die and getting 7
- Explain why probability cannot be less than 0 or greater than 1
- Classify the probability of raining tomorrow as 0, 0.5, or 1
- Give an example of an impossible event in your classroom
- Give an example of a certain event in daily life
11. Probability of Single Events
Probability = Number of favourable outcomes ÷ Total outcomes
Rolling a die, P(rolling 3) = 1/6
Practice Questions
- Find the probability of rolling a 4 on a 6-sided die
- Find the probability of tossing a coin and getting tails
- Find the probability of picking A from {A, B, C, D}
- Find the probability of rolling an even number on a die
- Find the probability of tossing a coin twice and getting two heads
12. Probability of Pair of Events
Pair events are often represented using tables.
| Red | Blue | |
|---|---|---|
| Circle | 2 | 3 |
| Square | 1 | 4 |
Practice Questions
- Using the table above, find P(Circle and Red)
- Find P(Square and Blue)
- Calculate the probability of picking a red shape (any type)
- Calculate the probability of picking a circle (any color)
- Create your own table for {Green, Yellow} × {Triangle, Hexagon} and find P(Triangle and Green)
13. Dependent and Independent Events
Independent Events
- One event does not affect the other
- Example: Tossing two coins
Dependent Events
- One event affects the outcome of the other
- Example: Picking cards without replacement
Practice Questions
- Give one real-life example of independent events
- Give one real-life example of dependent events
- Explain why tossing two coins is independent
- Explain why picking cards without replacement is dependent
- Identify whether the following is independent or dependent: Rolling a die twice without changing the die
14. Theoretical vs Experimental Probability
Theoretical Probability
- Based on all possible outcomes
- Calculated before an experiment
Experimental Probability
- Based on actual results of an experiment
- May change as number of trials increases
Practice Questions
- Calculate theoretical probability of rolling a 5 on a die
- Explain why experimental probability may differ from theoretical probability
- Conduct a small experiment tossing a coin 10 times and find experimental probability of heads
- Compare your experimental probability with theoretical probability for the coin toss
- Give an example of a situation where experimental probability is more useful than theoretical probability
IB MYP 2 – Unit 3: Ratio & Percentages
1. Ratio
A ratio compares two or more quantities of the same type.
- Written using : or as a fraction
- Order is important
This means for every 3 boys, there are 5 girls.
Simplifying Ratios
- Divide all parts by the highest common factor (HCF)
HCF of 12 and 18 = 6
= 2 : 3
Practice Questions
- Simplify the ratio 15 : 25
- For every 4 apples, there are 9 oranges. Write the ratio as a fraction
- Divide 24 pencils between two students in the ratio 5:7. How many pencils does each get?
- Simplify the ratio 18:30:12
- Explain why the order of numbers matters in a ratio
2. Proportion
Two ratios are in proportion if they are equal.
2 : 3 = 4 : 6
2/3 = 4/6
Checking Proportion
- Cross multiply
3 × 10 = 30
5 × 6 = 30
Therefore, they are in proportion.
Practice Questions
- Check if 4 : 7 and 12 : 21 are in proportion
- Determine if 5 : 8 and 10 : 16 are in proportion
- Write two ratios that are in proportion
- Explain why cross multiplication works to check proportion
- Check if 2 : 3 and 5 : 7 are in proportion
3. Problem Solving with Ratios
Sharing Quantities in a Given Ratio
- Add all parts of the ratio
- Find the value of one part
- Multiply accordingly
Total parts = 2 + 3 = 5
Value of 1 part = 600 ÷ 5 = 120
Shares = 2 × 120 = ₹240, 3 × 120 = ₹360
Practice Questions
- Divide ₹900 in the ratio 3 : 2
- Share 84 candies in the ratio 5 : 7
- Divide 120 liters of juice in the ratio 4 : 6
- Explain the steps to solve a ratio problem like this
- Divide ₹750 in the ratio 3 : 5 : 7
4. Direct and Inverse Variation
Direct Variation
- As one quantity increases, the other increases
- As one decreases, the other decreases
Cost ∝ Number of items
5 pens cost ₹50 → 1 pen costs ₹10
8 pens cost = 8 × 10 = ₹80
Inverse Variation
- As one quantity increases, the other decreases
Workers ∝ 1 / Time
6 workers take 10 days
12 workers take = (6 × 10) ÷ 12 = 5 days
Practice Questions
- Cost of 12 pens is ₹120. Find the cost of 1 pen (Direct Variation)
- 6 machines produce 120 units in 8 hours. How long will 4 machines take?
- 10 workers can complete a job in 15 days. Find time for 15 workers (Inverse Variation)
- Identify if the following is direct or inverse: Speed ∝ Time to travel 100 km
- Write an example of a direct variation in daily life
Graph Transformations
A transformation changes the position or orientation of a graph or shape on the coordinate plane without changing its size or shape. In MYP 2, we mainly study:
- Translations
- Reflections
- Rotations
1. Translations on a Graph
A translation moves a graph from one place to another without flipping, turning, or resizing it. Every point moves the same distance in the same direction.
Key idea: Translations change position only.
Translation Rule
A translation is written as:
(x, y) → (x + a, y + b)
acontrols movement left or rightbcontrols movement up or down
Direction and Signs
- Right → add to
x - Left → subtract from
x - Up → add to
y - Down → subtract from
y
Example: Translating a Point
Translate point A(2, 3) 4 units right and 1 unit down.
(x, y) → (x + 4, y − 1)
New point: A′(6, 2)
Translating a Shape
To translate a shape:
- Write the coordinates of every vertex
- Apply the translation rule to each point
- Plot the new points
- Join them in the same order
2. Reflections on a Graph
A reflection flips a graph across a line called the mirror line. The most common mirror lines are the x-axis and y-axis.
Reflection in the x-axis
The x-coordinate stays the same, but the y-coordinate changes sign.
(x, y) → (x, −y)
Reflection in the y-axis
The y-coordinate stays the same, but the x-coordinate changes sign.
(x, y) → (−x, y)
Example
Reflect point B(−3, 4) in the y-axis.
New point: B′(3, 4)
Important: Reflections reverse orientation (the shape looks flipped).
3. Rotations on a Graph
A rotation turns a graph around a fixed point called the center of rotation. In MYP 2, rotations are usually about the origin (0,0).
Common Rotations About the Origin
-
90° anticlockwise:
(x, y) → (−y, x) -
180° rotation:
(x, y) → (−x, −y) -
90° clockwise:
(x, y) → (y, −x)
Example: 180° Rotation
Rotate point C(5, −2) by 180° about the origin.
New point: C′(−5, 2)
Rotations change orientation but keep size and shape the same.
Summary Table
- Translation: slide (position changes)
- Reflection: flip (orientation reverses)
- Rotation: turn around a point
5. Rates and Unit Rates
A rate compares two quantities with different units.
- Speed = distance ÷ time
- Cost per item
Unit Rate
Rate for one unit.
300 km in 5 hours
Speed = 300 ÷ 5 = 60 km/h
Practice Questions
- A car travels 450 km in 9 hours. Find speed in km/h
- Cost of 15 pens is ₹75. Find cost per pen
- A person earns ₹1200 in 8 days. Find earnings per day
- Water tank fills 180 liters in 3 minutes. Find liters per minute
- Explain the difference between a rate and a unit rate
6. Percentages
Percentage means per hundred.
25% = 25/100 = 0.25
Percentage of a Quantity
= (20 ÷ 100) × 150
= 30
Practice Questions
- Find 15% of 200
- Convert 45% to a decimal
- Calculate 30% of 500
- Express 0.75 as a percentage
- If 60 is 20% of a number, find the number
7. Percentage Increase and Decrease
Percentage Increase
Increase = 10%
Increase amount = 10% of 500 = ₹50
New price = ₹550
Percentage Decrease
Decrease = 15%
Decrease amount = 120
New price = ₹680
Practice Questions
- Increase ₹400 by 12%
- Decrease ₹600 by 20%
- The price of an item increases from ₹250 to ₹300. Find the percentage increase
- The price decreases from ₹500 to ₹425. Find the percentage decrease
- Explain why percentage change is always calculated on the original value
8. Discount
A discount is a reduction in the marked price.
Marked price = ₹2000
Discount = 20%
Discount amount = 400
Selling price = ₹1600
Practice Questions
- Marked price = ₹1500, discount = 10%. Find selling price
- Marked price = ₹2500, discount = 25%. Find selling price
- If selling price is ₹800 after 20% discount, find the marked price
- Explain why discount is always calculated on marked price
- A shop offers 15% discount on ₹1200 item. Find the discounted price
9. Profit and Loss
Cost Price (CP)
Price at which an item is bought
Selling Price (SP)
Price at which an item is sold
Profit
Loss
Profit Percentage
Loss Percentage
Profit = ₹100
Profit % = (100 ÷ 500) × 100 = 20%
Practice Questions
- CP = ₹800, SP = ₹1000. Find profit and profit %
- CP = ₹1200, SP = ₹1000. Find loss and loss %
- CP = ₹450, SP = ₹500. Find profit %
- SP = ₹600, profit = ₹50. Find CP
- Explain why profit % is calculated on CP
IB MYP 2 – Unit 4: Algebra & Sequences
1. Sequences
A sequence is an ordered list of numbers that follows a rule or pattern.
2. Arithmetic Sequences
An arithmetic sequence is a sequence where the difference between consecutive terms is constant.
- The constant difference is called the common difference (d)
Common difference = +3
3. Geometric Sequences (Introduction)
A geometric sequence is a sequence where each term is multiplied by the same number to get the next term.
- The constant multiplier is called the common ratio (r)
Common ratio = ×2
Practice Questions
- Find the next three terms of 5, 8, 11, …
- Find the common difference of 7, 12, 17, 22, …
- Identify if 2, 6, 18, 54 is arithmetic or geometric
- Find the next three terms of 4, 12, 36, …
- Explain the difference between arithmetic and geometric sequences
4. Term-to-Term Rule
The term-to-term rule describes how you move from one term to the next.
Sequence: 1, 4, 9, 16, …
Rule: Add consecutive odd numbers (+3, +5, +7, …)
Practice Questions
- Find the term-to-term rule for the sequence 2, 4, 6, 8, …
- Sequence: 5, 10, 20, 40, … Identify the term-to-term rule
- Explain the difference between term-to-term and nth term rules
- Sequence: 3, 6, 12, 24, … Find the term-to-term rule
- Write a sequence with a term-to-term rule of +7
5. Position-to-Term Rule (nth Term)
The nth term rule gives a formula to find any term directly.
nth Term of an Arithmetic Sequence
a = 3, d = 4
nth term = 3 + (n − 1)4 = 4n − 1
Practice Questions
- Find the 10th term of 2, 5, 8, 11, …
- nth term of 7, 12, 17, 22, …
- Find the 15th term of 4, 9, 14, 19, …
- Write the nth term for 5, 10, 15, 20, …
- Explain how the nth term formula relates to the term-to-term rule
6. Algebraic Expressions
An algebraic expression contains numbers, variables, and operations.
Formation of Algebraic Expressions
Perimeter of a rectangle with length l and breadth b → 2(l + b)
Linear Expressions with More Than One Variable
Linear expressions have variables raised to the power of 1 only.
−4a + 7b
Substitution into Algebraic Expressions
Substitute the given values of variables and evaluate.
x = 4, y = 2
= 2(4) + 3(2) = 8 + 6 = 14
Practice Questions
- Form an algebraic expression for: 7 more than 3 times a number x
- Form an expression for the perimeter of a rectangle with length l and width w
- Evaluate 4a − 3b for a = 2, b = 5
- Evaluate 5x + 2y − 3 for x = 1, y = 4
- Explain why 2x² + 3x is not a linear expression
10. Simplifying Algebraic Expressions
Like terms have the same variables raised to the same powers.
Practice Questions
- Simplify: 4a + 7a − 3b + 2b
- Simplify: 5x − 2x + 3y − y
- Explain why 2x + 3xy cannot be simplified with 4x + 5xy
- Simplify: 7m − 3m + 2n − n
- Simplify: 6p + 2q − 4p + 5q
11. Division of Polynomials
Divide each term in the polynomial by the divisor.
= 3x + 2
Practice Questions
- (8x² + 12x) ÷ 4x
- (10a² + 5a) ÷ 5a
- (15y² − 5y) ÷ 5y
- (12m² + 8m − 4) ÷ 4
- (9x³ + 6x²) ÷ 3x²
12. Expanding Algebraic Expressions
Use the distributive law: a(b + c) = ab + ac
Practice Questions
- Expand: 5(a + 3)
- Expand: (x + 4)(x + 5)
- Expand: 2(3x + 7)
- Expand: (y + 2)(y + 3)
- Expand: (2a + 5)(a + 1)
13. Factorising Algebraic Expressions
Factorising is the reverse of expanding.
Practice Questions
- Factorise: 8a + 12
- Factorise: x² + 7x
- Factorise: 10y + 15
- Factorise: 6m² + 9m
- Factorise: 4p² + 8p
14. Changing the Subject of a Formula
Rearrange the formula to make a different variable the subject.
Make x the subject:
y − 3 = 2x
x = (y − 3)/2
Practice Questions
- Make y the subject: x = 3y + 4
- Make a the subject: P = 2a + b
- Make x the subject: 5x − 7 = 18
- Make t the subject: s = ut + ½at²
- Explain the steps to change the subject of a formula
15. Linear Equations
A linear equation has variables with highest power 1.
Practice Questions
- Identify whether 3x + 5 = 0 is a linear equation
- Is 2x² + 3x − 5 linear or non-linear?
- Write a linear equation for a line passing through (0, 3) with slope 2
- Check if y = 4x + 7 is linear
- Explain why x + y + z = 10 is considered linear
16. Solving Linear Equations
Transposition Method
3x = 15
x = 5
Elimination Method
x − y = 2
Adding equations:
2x = 12 → x = 6, y = 4
Practice Questions
- Solve 5x − 7 = 18 using transposition
- Solve 2x + 3y = 12 and x − y = 2 using elimination
- Solve 4a + 5 = 21 using transposition
- Solve x + y = 8, x − y = 2 using elimination
- Explain the difference between transposition and elimination methods
17. Linear Graphs (Introduction to y = mx + c)
The equation y = mx + c represents a straight line.
- m = slope (gradient)
- c = y-intercept
Slope = 2, y-intercept = 1
Practice Questions
- Find slope and y-intercept: y = 3x − 4
- Write equation for a line with slope 5 and y-intercept 2
- Graph y = −x + 3
- Explain what the slope tells you about the line
- Explain what the y-intercept represents on a graph
18. Distance-Time Graph (No Slope)
- Horizontal line → object at rest
- Straight rising line → constant speed
Practice Questions
- Draw a distance-time graph for an object at rest for 5 seconds
- Draw a graph for an object moving at 10 m/s for 6 seconds
- Explain the meaning of a horizontal line on a distance-time graph
- Explain the meaning of a steep slope on a distance-time graph
- Compare two objects moving at different constant speeds on the same graph
A distance–time graph shows how the distance travelled by an object changes with time.
Axes on a Distance–Time Graph
- X-axis: Time (seconds, minutes, or hours)
- Y-axis: Distance (metres or kilometres)
Key Types of Lines on a Distance–Time Graph
1. Horizontal Line (Object at Rest)
- Distance does not change as time increases
- The object is not moving
- Speed = 0
From 2 minutes to 6 minutes, the graph is horizontal at 40 m.
The object stayed at 40 m and was stationary.
2. Straight Sloping Line (Constant Speed)
- Distance increases uniformly with time
- The object is moving at a constant speed
- Steeper line → faster movement
the object is travelling at a constant speed.
3. Curve (Changing Speed – Awareness Only)
- Distance does not increase evenly
- Speed is changing
- Not required to calculate in MYP 2
Reading Information from the Graph
- Find distance travelled at a given time by reading the y-value
- Find time taken to reach a distance by reading the x-value
- Compare speeds by comparing steepness of lines
The object has travelled 100 m in 5 minutes.
Common Interpretation Questions (Criterion D)
- When was the object at rest?
- During which interval was the object moving fastest?
- How long did the object remain stationary?
- Describe the motion in words
“From 0 to 4 minutes, the object moved at a constant speed.
From 4 to 7 minutes, it remained stationary.”
Common Mistakes to Avoid
- Confusing distance with speed
- Assuming a higher graph means faster (steepness matters)
- Trying to calculate slope when not required